人生で役立つ Grimshaw’s Trick

概要

人生を生きていると一般化パレート分布のパラメータを最尤推定したいときがあります。しかしこの推定は2変数の非線形最適化問題を解く必要があり数値計算的に不安定なため人生も不安になります。そんなときにGrimshaw’s Trickを使えばこの問題を一元方程式の解を求める問題に帰着でき数値的に安定するので人生も安心です。本記事ではそんな人生に役立つGrimshaw’s Trickを紹介します。

1. はじめに

極値理論は確率変数の極値 (最大値または最小値) に関する理論である。 極値理論では1920年から1940年にかけて中心極限定理に似た美しい結果が得られた。 それは確率変数列の極値はその分布によらず3つのタイプの確率分布 (極値分布) に弱収束するというものである (Fisher–Tippett–Gnedenko定理)。 これは極値理論の大定理となったが、実データに対して極値分布のパラメータを推定するのは困難であった。 原因は期間ごとの極値をサンプルとして扱う必要があるため必然的にサンプルサイズが小さくなることに加えてパラメータが元の分布に依存することにある。 この問題を解決するために Peaks-Over-Threshold (POT) というアプローチが使われるようになった。 このアプローチは極値が従う分布を調べる代わりにピーク (設定した閾値を超える値) が従う確率分布を調べるというものである。 1970年代に POT アプローチにおける重要な定理が証明された。 ピークが従う確率分布は元の分布によらず一般化パレート分布で近似できるというものである (Pickands–Balkema–de Haan定理)。 この定理により極値理論における次の関心事は一般化パレート分布のパラメータをどうやって推定するのかに移った。 この問題に対してモーメント法によるいくつかの推定法が提案されたが、推定量が理論的に良い性質をもつ最尤法による推定手法が望まれた。 しかし、一般化パレート分布の最尤推定のためには2変数の非線形最適化問題を解く必要があり数値計算の安定性の問題をはらむ。 本記事ではより安定した数値計算のために Grimshaw [1993] で提案された変数変換とその解法を紹介する。

2. 一般化パレート分布の最尤推定

一般化パレート分布は1変数の連続型の確率分布であり、次の確率密度関数をもつ。

$$ f(x) = \begin{cases} \frac{1}{\sigma} \left( 1 + \frac{\gamma}{\sigma}x \right) ^ {-\left(1 + \frac{1}{\gamma}\right)} & \gamma \neq 0 \\ \frac{1}{\sigma} \exp\left( -\frac{x}{\sigma} \right) & \gamma = 0 \end{cases} $$

ただし、 は尺度パラメータ、 は形状パラメータである。

の場合、 の指数分布となるので、 の最尤推定値はデータの平均値である。

の場合、データ が与えられたとき、対数尤度関数は次になる。

$$ \begin{align} LogLik(\sigma, \gamma) &= \sum_{i=1}^n \log\left( \frac{1}{\sigma} \left( 1 + \frac{\gamma}{\sigma}x_i \right) ^ {-\left(1 + \frac{1}{\gamma}\right)} \right) \\ &= \sum_{i=1}^n -\log \sigma + \sum_{i=1}^n -\left(1 + \frac{1}{\gamma}\right) \log \left( 1 + \frac{\gamma}{\sigma}x_i \right) \\ &= -n \log \sigma - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \log \left( 1 + \frac{\gamma}{\sigma}x_i \right)\\ \end{align} $$

この対数尤度関数を最大にするような と を求めることが本記事の目的である。

ここで、パラメータ と のとる範囲を考えてみよう。 対数尤度の式の より、すべての に対して である必要がある。 これは ならば自然に満たす。 の場合、データ の最大値で成り立てば他も自然に満たすため、

$$ \begin{align} & \sigma > -\gamma \max(X) \\ \end{align} $$

という条件になる。したがって、パラメータのとる領域は次図のように制限される。

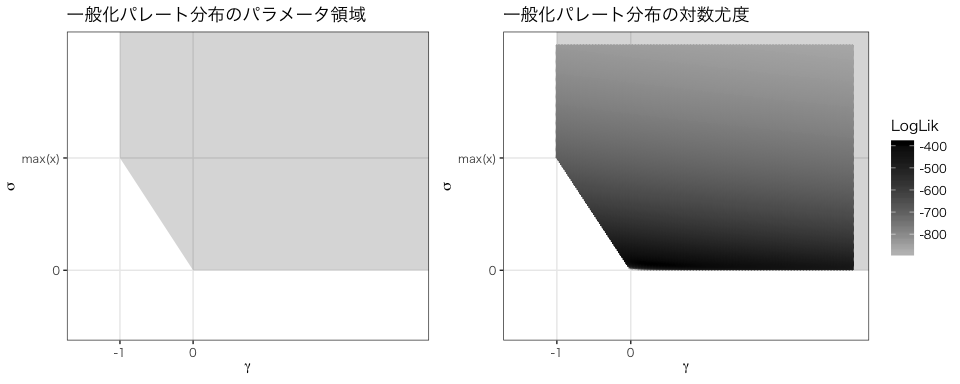
右図に , のときの対数尤度を示した。 最適なパラメータは境界付近にあり、境界付近では勾配が急であることがわかる。 このような場合に勾配を使った数値最適化は不安定になりやすい。 また、後述するように を特別な場合として扱う必要があるという問題もある。

1980年代に一般化パレート分布に対する最尤推定アルゴリズムは多数提案された (DuMouchel [1983], Davison [1984], R. L. Smith [1984, 1987], J. A. Smith [1986], Joe [1984]) が、どれも数値安定性の問題をはらんでいた。 Grimshaw [1993] は、2パラメータの最適化を行うのではなく、変数変換により一元方程式の求根問題に帰着することで数値的に安定した解を得る方法を示した。

3. Grimshaw's Trick

対数尤度関数を最大化するために、勾配が 0 となる と を求めたい ()。 まずはそれぞれの偏微分を導出しよう。

$$ \begin{align} \frac{\partial LogLik(\sigma, \gamma)}{\partial \sigma} &= \frac{\partial}{\partial \sigma} \left( -n \log \sigma - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \log \left( 1 + \frac{\gamma}{\sigma}x_i \right) \right) \\ &= -n \frac{1}{\sigma} - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{1 + \frac{\gamma}{\sigma}x_i} \left( - \frac{\gamma}{\sigma^2} x_i\right) \\ &= - \frac{n}{\sigma} + \left(1 + \frac{1}{\gamma}\right) \frac{1}{\sigma} \sum_{i=1}^n \frac{\frac{\gamma}{\sigma}x_i}{1 + \frac{\gamma}{\sigma}x_i} \\ &= - \frac{n}{\sigma} + \left(1 + \frac{1}{\gamma}\right) \frac{1}{\sigma} \sum_{i=1}^n \frac{1 + \frac{\gamma}{\sigma}x_i - 1}{1 + \frac{\gamma}{\sigma}x_i} \\ &= - \frac{n}{\sigma} + \left(1 + \frac{1}{\gamma}\right) \frac{1}{\sigma} \sum_{i=1}^n 1 + \left(1 + \frac{1}{\gamma}\right) \frac{1}{\sigma} \sum_{i=1}^n \frac{-1}{1 + \frac{\gamma}{\sigma}x_i} \\ &= - \frac{n}{\sigma} + \left(1 + \frac{1}{\gamma}\right) \frac{n}{\sigma} - \frac{1}{\sigma} \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{1 + \frac{\gamma}{\sigma}x_i} \\ &= \frac{n}{\gamma\sigma} - \frac{1}{\sigma} \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{1 + \frac{\gamma}{\sigma}x_i} \\ \frac{\partial LogLik(\sigma, \gamma)}{\partial \gamma} &= \frac{\partial}{\partial \gamma} \left( -n \log \sigma - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \log \left( 1 + \frac{\gamma}{\sigma}x_i \right) \right) \\ &= \frac{1}{\gamma^2} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{\frac{1}{\sigma}x_i}{1 + \frac{\gamma}{\sigma}x_i} \\ &= \frac{1}{\gamma^2} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{\gamma} \frac{1 + \frac{\gamma}{\sigma}x_i - 1}{1 + \frac{\gamma}{\sigma}x_i} \\ &= \frac{1}{\gamma^2} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{\gamma} - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{\gamma} \frac{- 1}{1 + \frac{\gamma}{\sigma}x_i} \\ &= \frac{1}{\gamma^2} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) - \left(1 + \frac{1}{\gamma}\right) \frac{n}{\gamma} + \frac{1}{\gamma} \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{ 1}{1 + \frac{\gamma}{\sigma}x_i} \\ \end{align} $$

したがって、一般化パレート分布の最尤推定を行うには次の連立方程式を解けばよい。

$$ \begin{cases} \begin{align} \frac{n}{\gamma\sigma} - \frac{1}{\sigma} \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{1 + \frac{\gamma}{\sigma}x_i} &= 0 & (1)\\ \frac{1}{\gamma^2} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) - \left(1 + \frac{1}{\gamma}\right) \frac{n}{\gamma} + \frac{1}{\gamma} \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{ 1}{1 + \frac{\gamma}{\sigma}x_i} &= 0 & (2)\\ \end{align} \end{cases} $$

実はこの偏微分の導出過程ですでに Grimshaw のアイデアが使われている。 連立方程式の左辺の後半部分が同じ形になるように式変形を行った。 式 (1) に をかけ、式 (2) に をかけるとこの部分が完全に同じになる。

$$ \begin{cases} \begin{align} \frac{n}{\gamma} - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{1}{1 + \frac{\gamma}{\sigma}x_i} &= 0\\ \frac{1}{\gamma} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) - n - \frac{n}{\gamma} + \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \frac{ 1}{1 + \frac{\gamma}{\sigma}x_i} &= 0\\ \end{align} \end{cases} $$

上式と下式を足し合わせることで次の式が得られる。

$$ \begin{align} & \frac{1}{\gamma} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) - n = 0 &\\ & \gamma = \frac{1}{n} \sum_{i=1}^n\log \left( 1 + \frac{\gamma}{\sigma}x_i \right) & (3) \end{align} $$

式 (3) は最適なパラメータが満たすべき条件となる。

例えば、, の場合、式 (3) は次図の青線になる。 この線上に最適パラメータ (赤点) が存在する。 は必ず条件を満たすが、特別に扱う必要があり、これも上記の最適化問題を難しくしている。

そこで、Grimshaw は による変数変換を提案した。 を に写すことで次の良い性質が得られる。

• 変換 は を除いて全単射である。
• ならば であり、特別な場合が1点に集約される。
• 解の領域がパラメータに依存せず矩形になる ()。
• 勾配が急になる境界は 付近のみである。

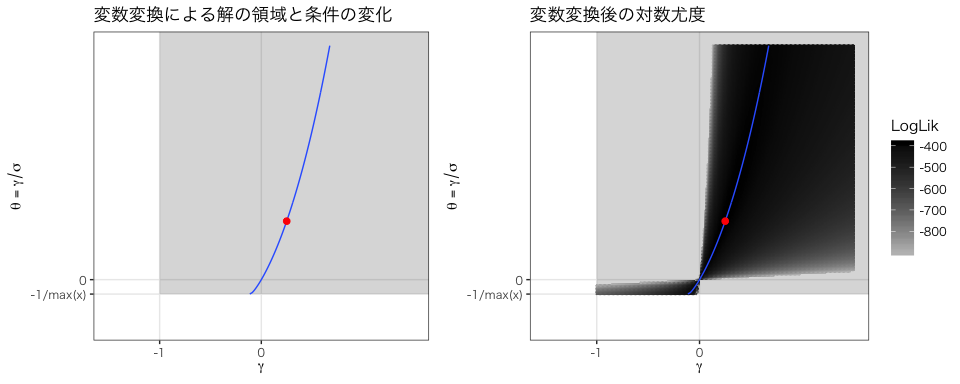
この変換により、最適条件を満たす場合、式 (3) から は によって定まる。

$$ \begin{align} \gamma &= \frac{1}{n} \sum_{i=1}^n\log \left( 1 + \theta x_i \right) \end{align} $$

したがって、解を求めるために連立方程式を解く必要はなくなり、最適な だけを求めれば良い。

具体的には2変数の尤度関数を だけの関数に変換する。

$$ \begin{cases} \gamma = \frac{1}{n} \sum_{i=1}^n\log \left( 1 + \theta x_i \right) \\ \sigma = \frac{\gamma}{\theta} \end{cases} $$

$$ \begin{align} LogLik(\theta) &= -n \log \sigma - \left(1 + \frac{1}{\gamma}\right) \sum_{i=1}^n \log \left( 1 + \frac{\gamma}{\sigma}x_i \right)\\ &= -n \log \left( \frac{\gamma}{\theta} \right) - \left(1 + \frac{1}{\gamma}\right) n\gamma\\ &= -n \log \left( \frac{1}{\theta} \frac{1}{n} \sum_{i=1}^n\log \left( 1 + \theta x_i \right) \right) - n\gamma -n \\ &= -n \log \left( \frac{1}{n} \sum_{i=1}^n \frac{1}{\theta} \log \left( 1 + \theta x_i \right) \right) - \sum_{i=1}^n\log \left( 1 + \theta x_i \right) -n \\ \end{align} $$

このように、尤度関数を注目したいパラメータだけの関数として表したものをプロファイル尤度という。 一般化パレート分布の最尤推定の問題は、この1パラメータのプロファイル対数尤度を最大化する問題となる。

プロファイル対数尤度の微分を求める。

$$ \begin{align} \frac{d\ LogLik(\theta)}{d\theta} &= -n \frac{ \frac{1}{n} \sum_{i=1}^n \left( -\frac{1}{\theta^2} \log(1+\theta x_i) + \frac{1}{\theta}\frac{x_i}{1+\theta x_i} \right) }{ \frac{1}{n} \sum_{i=1}^n \frac{1}{\theta} \log \left( 1 + \theta x_i \right) } - \sum_{i=1}^n \frac{x_i}{1 + \theta x_i} \\ &= -n \frac{ - \sum_{i=1}^n \frac{1}{\theta^2} \log(1+\theta x_i) + \sum_{i=1}^n \frac{1}{\theta}\frac{x_i}{1+\theta x_i} }{ \sum_{i=1}^n \frac{1}{\theta} \log \left( 1 + \theta x_i \right) } - \sum_{i=1}^n \frac{x_i}{1 + \theta x_i} \\ &= \frac{n}{\theta} -n \frac{\sum_{i=1}^n \frac{x_i}{1+\theta x_i}}{\sum_{i=1}^n \log \left( 1 + \theta x_i \right)} - \left( \frac{n}{\theta} - \frac{1}{\theta} \sum_{i=1}^n \frac{1}{1+\theta x_i} \right)\\ &= -n\frac{\left( \frac{n}{\theta} - \frac{1}{\theta} \sum_{i=1}^n \frac{1}{1+\theta x_i} \right)}{\sum_{i=1}^n \log \left( 1 + \theta x_i \right)} + \frac{1}{\theta} \sum_{i=1}^n \frac{1}{1+\theta x_i} \\ &= -\frac{n}{\theta}\left( n - \sum_{i=1}^n \frac{1}{1+\theta x_i} \right) \left( \frac{1}{\sum_{i=1}^n \log \left( 1 + \theta x_i \right)}\right) + \frac{1}{\theta} \sum_{i=1}^n \frac{1}{1+\theta x_i} \end{align} $$

だだし、次を用いた。

$$ \begin{align} \sum_{i=1}^n \frac{x_i}{1+\theta x_i} &= \frac{1}{\theta} \sum_{i=1}^n \frac{1 + \theta x_i + 1}{1+\theta x_i} \\ &= \frac{1}{\theta} \sum_{i=1}^n 1 + \frac{1}{\theta} \sum_{i=1}^n \frac{-1}{1+\theta x_i} \\ &= \frac{n}{\theta} - \frac{1}{\theta} \sum_{i=1}^n \frac{1}{1+\theta x_i} \end{align} $$

プロファイル対数尤度の微分が 0 になるには次を満たせばよい。

$$ \begin{align} -\frac{n}{\theta}\left( n - \sum_{i=1}^n \frac{1}{1+\theta x_i} \right) \left( \frac{1}{\sum_{i=1}^n \log \left( 1 + \theta x_i \right)}\right) + \frac{1}{\theta} \sum_{i=1}^n \frac{1}{1+\theta x_i} &= 0 \\ \left( n - \sum_{i=1}^n \frac{1}{1+\theta x_i} \right) \left( \frac{1}{\sum_{i=1}^n \log \left( 1 + \theta x_i \right)}\right) - \frac{1}{n} \sum_{i=1}^n \frac{1}{1+\theta x_i} &= 0 \\ \left( n - \sum_{i=1}^n \frac{1}{1+\theta x_i} \right) - \frac{1}{n} \sum_{i=1}^n \frac{1}{1+\theta x_i} \left( \sum_{i=1}^n \log \left( 1 + \theta x_i \right)\right) &= 0 \\ n - \left( \sum_{i=1}^n \frac{1}{1+\theta x_i} \right) \left( 1 + \frac{1}{n} \sum_{i=1}^n \log \left( 1 + \theta x_i \right)\right) &= 0 \\ \left( \frac{1}{n}\sum_{i=1}^n \frac{1}{1+\theta x_i} \right) \left( 1 + \frac{1}{n} \sum_{i=1}^n \log \left( 1 + \theta x_i \right)\right) &= 1 \\ \end{align} $$

ここで

$$ \begin{align} u(\theta) &= \frac{1}{n}\sum_{i=1}^n \frac{1}{1+\theta x_i} \\ v(\theta) &= 1 + \frac{1}{n} \sum_{i=1}^n \log \left( 1 + \theta x_i \right) \end{align} $$

とおくと

$$ \begin{align} u(\theta) v(\theta) &= 1 & (4) \end{align} $$

と表せる。

この方程式を満たす を求めることで、一般化パレート分布の2つのパラメータを次の式で計算できる。

$$ \begin{align} \gamma &= \frac{1}{n} \sum_{i=1}^n \log \left( 1 + \theta x_i \right) \\ \sigma &= \frac{\gamma}{\theta} \end{align} $$

これが Grimshaw's Trick である。

4. 解の存在

Grimshaw's Trick により一般化パレート分布の最尤推定は式 (4) の方程式を解く問題に帰着された。

ここで

$$ h(\theta) = u(\theta) v(\theta) - 1 $$

とおくと、 の解を求めればよい。

次図に , のときのプロファイル対数尤度と を示す。

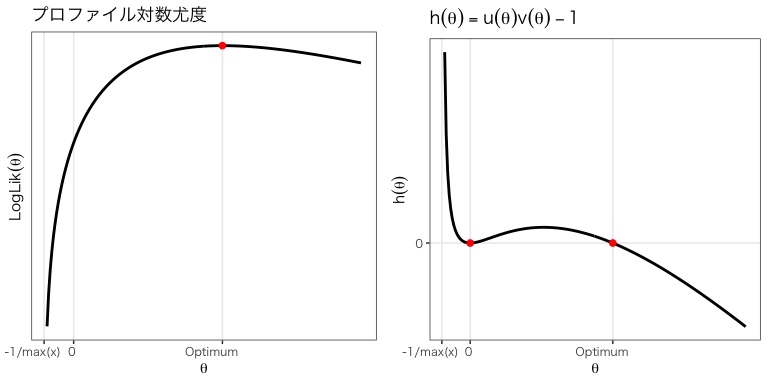
方程式 に解が存在することを示そう。

まず ならば , なので となる。 したがって は常に解である。 ただし上図からわかるように はプロファイル尤度を最大にするとは限らない。

以外に解が存在することは次で示すことができる。

$$ \begin{align} \theta \rightarrow \frac{-1}{\max(X)} &\ \Rightarrow\ h(\theta) \rightarrow \infty & (a)\\ \theta > 2\frac{\bar{X} - \min(X)}{\min(X)^2} &\ \Rightarrow\ h(\theta) < 0 & (b) \\ \theta \rightarrow 0 &\ \Rightarrow \ h'(\theta) = 0 & (c) \end{align} $$

ただし はデータ の平均値である。

これらの結果より、 が で鞍点でなければ次の範囲内に となる が 以外に1つ以上あることがわかる。

$$ \begin{align} &-\frac{1}{\max(X)} < \theta < 2\frac{\bar{X} - \min(X)}{\min(X)^2} & (5) \\ \end{align} $$

式 (a) - (c) の証明については Grimshaw [1993] では次のように書かれている。

Proof. The results are straightforward.
(訳：この証明は非常に難しい）

したがって、本記事では証明しないことにする¹。

一方、 の解が1つである保証はない。 そのため次の手順でプロファイル対数尤度が最大となる を見つける。

1. 方程式 のすべての解を求める。
2. すべての解に対して を計算し、最大になる を選ぶ。

ただし、複数の根のある方程式の解法は一般には知られていない²。 Grimshaw [1993] では方程式 に対して、解の探索区間を細かく区切り、ニュートン・ラフソン法を繰り返し用いることですべての解を求める手順が示されている。 この手順はR言語では mev パッケージの gp.fit(method="Grimshaw") で実行できる。

# データの生成
sigma <- 2
gamma <- 0.25

set.seed(314)
x <- POT::rgpd(200, 0, sigma, gamma)

# Grimshaw の手順でパラメータを最尤推定
library(mev)
fit <- gp.fit(x, 0, method="Grimshaw")
est_sigma <- unname(fit$estimate[1])
est_gamma <- unname(fit$estimate[2])

# 推定結果の表示
c(sigma = est_sigma, gamma = est_gamma)

##     sigma     gamma 
## 1.9039251 0.2957402

5. Sifferらの求根法

方程式 のすべての解を求める方法として、Siffer et al. [2017] で提案された方法が面白いので紹介したい。

式 (5) より、解の探索範囲として次の2つの区間を考える。ただし は非常に小さい正の実数とする。

$$ \begin{align} I_1 &= \left[-\frac{1}{\max(X)} + \varepsilon,\ -\varepsilon \right] \\ I_2 &= \left[\varepsilon,\ 2\frac{\bar{X} - \min(X)}{\min(X)^2} - \varepsilon\right] \\ \end{align} $$

この2つの区間において、次で定義する 変数関数の最小化を行う。

$$ f(\theta_1, \dots, \theta_K) = h(\theta_1)^2 + \dots h(\theta_K)^2 $$

すなわち、次の最小化問題を解く。

$$ \min_{\theta_1, \dots, \theta_K} \sum_{k=1}^K h(\theta_k)^2 $$

ただし、 の初期値をそれぞれの区間で散らばるように設定する。 これにより は の異なる局所解に収束することが期待される。 したがって、この最小化問題を解くことで、最大で 個の根が得られる。

2つの区間それぞれに対して最小化問題を解き、得られた 個の根に 0 (常に解) を加える。 こうして得られた 個の根に対してプロファイル尤度を計算し、尤度が最大となる根を選択するというのが Sifferらの提案した方法である。

Siffer et al. [2017] では , 、最適化手法として L-BFGS-B法が用いられている。

R言語では Sifferらの方法は次のように実装できる。

#' 一般化パレート分布の最尤推定を Sifferらの方法で行う関数
#'
#' @param x データを数値ベクトルとして入力
#' @param K デフォルトは 10
#' @param epsilon 境界を探索範囲から外すための微小値。デフォルトは 10^-8
#' @return パラメータの最尤推定値 c(sigma, gamma) 
gp.fit_siffer <- function(x, K = 10, epsilon = 10^-8) {
  # 式 (4) の方程式
  u <- function(theta) mean(1 / (1 + theta * x))
  v <- function(theta) 1 + mean(log(1 + theta * x))
  h <- function(theta) u(theta) * v(theta) - 1
  
  # 最適化目的関数
  fn <- function(theta_K, logged=FALSE) {
    if(logged) theta_K <- exp(theta_K)
    sum(vapply(theta_K, h, double(1))^2)
  }
  
  # 解の範囲
  lower_bound <- -1 / max(x)
  upper_bound <- 2 * (mean(x) - min(x)) / min(x)^2

  theta_range1 <- c(lower_bound + epsilon, -epsilon)
  theta_range2 <- c(epsilon, upper_bound)

  # 初期値の設定
  theta_init1 <- seq(lower_bound, 0, length.out = K+2)[-c(1, K+2)]
  theta_init2 <- seq(log(epsilon), log(upper_bound), length.out = K+2)[-c(1, K+2)]

  # 最適化の実行
  opt1 <- optim(theta_init1, fn = fn, method = "L-BFGS-B",
                lower = theta_range1[1], upper = theta_range1[2])
  opt2 <- optim(theta_init2, fn = fn, logged = TRUE, method = "L-BFGS-B",
                lower = log(theta_range2[1]), upper = log(theta_range2[2]))

  # 最適解 (推定値の候補)
  opt_theta_K <- unique(c(opt1$par, 0, exp(opt2$par)))

  # プロファイル対数尤度
  n <- length(x)
  profileLogLik <- function(theta) {
    -n * log(mean(log(1 + theta * x))/theta) - n * mean(log(1 + theta * x)) - n
  }

  # 最適解のうちプロファイル対数尤度が最大のものを推定値とする
  pLLs <- vapply(opt_theta_K, profileLogLik, double(1))
  est_theta <- opt_theta_K[which.max(pLLs)]
  
  # パラメータの引き戻し
  est_gamma <- mean(log(1 + est_theta * x))
  est_sigma <- est_gamma / est_theta
  
  # 結果の返却
  c(sigma = est_sigma, gamma = est_gamma)
}

推定を実行してみる。

# データの生成
sigma <- 2
gamma <- 0.25

set.seed(314)
x <- POT::rgpd(200, 0, sigma, gamma)

# Sifferらの方法でパラメータを最尤推定
gp.fit_siffer(x)

##     sigma     gamma 
## 1.9040107 0.2956953

Grimshaw の手順と同様の結果が得られた。

6. まとめ

「人生を安定させるにはまず数値計算を安定させよ」という格言があります³。 本記事では人生を安定させるための第一歩として、一般化パレート分布の最尤推定を安定させるための Grimshaw's Trick を紹介しました。 あなたの人生で一般化パレート分布を最尤推定したい、そんなときに役立つ知識が得られたのではないかと思います。

参考文献

• Scott D. Grimshaw (1993) Computing Maximum Likelihood Estimates for the Generalized Pareto Distribution, Technometrics, 35:2, 185-191, DOI: https://doi.org/10.1080/00401706.1993.10485040
• Alban Siffer, Pierre-Alain Fouque, Alexandre Termier, and Christine Largouet. 2017. Anomaly Detection in Streams with Extreme Value Theory. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '17). ACM, New York, NY, USA, 1067-1075. DOI: https://doi.org/10.1145/3097983.3098144

付録

式 (b) を証明する。

$$ \begin{align} \theta > 2\frac{\bar{X} - \min(X)}{\min(X)^2} &\ \Rightarrow\ h(\theta) \lt 0 & (b) \\ \end{align} $$

イエンセンの不等式より

$$ \begin{align} v(\theta) &= 1 + \frac{1}{n} \sum_{i=1}^n \log (1 + \theta x_i)\\ &\leq 1 + \log(1 + \theta \bar{X}) \end{align} $$

また、任意の に対して より

$$ \begin{align} u(\theta) &= \frac{1}{n} \sum_{i=1}^n \frac{1}{1 + \theta x_i} \\ &\leq \frac{1}{n} \sum_{i=1}^n \frac{1}{1 + \theta \min(X)} \\ &\leq \frac{1}{1 + \theta \min(X)} \end{align} $$

したがって、

$$ \begin{align} h(\theta) &= u(\theta)v(\theta) - 1 \\ &\leq \frac{1 + \log(1 + \theta \bar{X})}{1 + \theta \min(X)} - 1 \\ &= \frac{1 + \log(1 + \theta \bar{X}) - 1 - \theta \min(X)}{1 + \theta \min(X)} \\ &= \frac{\log(1 + \theta \bar{X}) - \theta \min(X)}{1 + \theta \min(X)} \\ \end{align} $$

分子が負ならば である。よって

$$ \begin{align} \frac{2(\bar{X} -\min(\theta))}{\min(X)^2} < \theta &\ \Rightarrow\ \bar{X} < \min(X) + \frac{1}{2}\theta\min(X)^2 \\ &\ \Rightarrow\ 1 + \theta \bar{X} < 1 + \theta\min(X) + \frac{1}{2}\theta^2\min(X)^2 \\ &\ \Rightarrow\ 1 + \theta \bar{X} < \exp(\theta\min(X)) \\ &\ \Rightarrow\ \log (1 + \theta \bar{X}) < \theta\min(X) \\ &\ \Rightarrow\ h(\theta) < 0 \\ \end{align} $$

以上で証明された。ただし、指数関数のマクローリン展開

$$ \begin{align} \exp(x) &= 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + \dots \\ &> 1 + x + \frac{1}{2} x^2 \end{align} $$

をもちいた。

---

1. これはウィットに富んだジョークである。(b) の証明は付録に示す。↩

2. 多項式の場合はスツルム (Sturm) の解法が知られている。↩

3. 私が考えた格言です。↩