マイナーだけど最強の統計的検定 Brunner-Munzel 検定

対応のない 2 群間の量的検定手法として、最も有名なのは Student の t 検定でしょうか。
以前、Student の t 検定についての記事を書きました。

• 小標本問題と t検定 - ほくそ笑む

しかし、Student の t 検定は、等分散性を仮定しているため、不等分散の状況にも対応できるように、Welch の t 検定を使うのがセオリーとなっています。

ただし、これら 2つの検定は分布の正規性を仮定しているため、正規性が仮定できない状況では、Mann-Whitney の U検定というものが広く使われています。

Mann-Whitney の U検定は、正規性を仮定しないノンパラメトリック検定として有名ですが、不等分散の状況でうまく検定できないという問題があることはあまり知られていません。

今日は、これらの問題をすべて解決した、正規性も等分散性も仮定しない最強の検定、Brunner-Munzel 検定を紹介し、その検定精度について調査してみます。

Brunner-Munzel 検定

Brunner-Munzel 検定の理論的な側面は、奥村先生のホームページが詳しいです。

すなわち、Mann-Whitney の U検定は、2群間の分布の形状が同じであるという仮定を持つのに対し、Brunner-Munzel 検定は、分布が同じことは仮定せず、両群から一つずつ値を取り出したとき、どちらが大きい確率も等しいという帰無仮説を検定するというものです。

Brunner-Munzel 検定を R で行うには、lawstat パッケージの brunner.munzel.test() 関数を使います。

library(lawstat)
x = c(1,2,1,1,1,1,1,1,1,1,2,4,1,1)
y = c(3,3,4,3,1,2,3,1,1,5,4)
brunner.munzel.test(x,y)

##  Brunner-Munzel Test
## 
## data:  x and y
## Brunner-Munzel Test Statistic = 3.138, df = 17.68, p-value = 0.005786
## 95 percent confidence interval:
##  0.5952 0.9827
## sample estimates:
## P(X<Y)+.5*P(X=Y) 
##            0.789

本記事では、不等分散の状況で Brunner-Munzel 検定がどれほどの検定精度を持つのかを調査します。
その際、比較対象として、Student の t 検定、Welch の t 検定、Mann-Whitney の U 検定についても検定精度を調査します。

それぞれの検定における仮定は次の通りです。

手法	正規性	等分散性
Student’s t	要	要
Welch’s t	要	不要
Mann-Whitney	不要	要
Brunner-Munzel	不要	不要

1. 正規分布

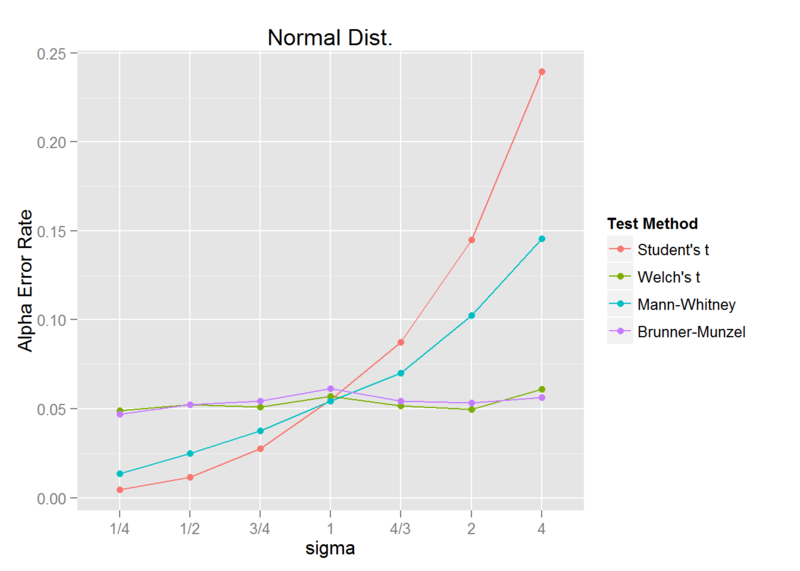
まずは、正規分布に対する検定精度を調査します。 標準偏差 1 の正規分布に対して、標準偏差を 1/4, 1/2, 3/4, 1, 4/3, 2, 4 と変化させた正規分布との検定をそれぞれ繰り返し、第一種の過誤(alpha error rate)を調査します。

sigma_ratio <- c("1/4", "1/2", "3/4", "1", "4/3", "2", "4")
sigma1 <- c(1/4, 1/2, 3/4, 1, 4/3, 2, 4)
sigma2 <- 1
iter_num <- 2000

library(pforeach)
library(lawstat)
pforeach(sigma=sigma1, .c=rbind)({
  npforeach(i=seq_len(iter_num), .c=rbind)({
    x1 <- rnorm(15, mean = 5, sd = sigma)
    x2 <- rnorm(45, mean = 5, sd = sigma2)
    student <- t.test(x1, x2, var.equal = TRUE)$p.value <= 0.05
    welch <- t.test(x1, x2, var.equal = FALSE)$p.value <= 0.05
    MH <- wilcox.test(x1,x2)$p.value <= 0.05
    BM <- brunner.munzel.test(x1, x2)$p.value <= 0.05
    data.frame(`Student's t`=student, `Welch's t`=welch, `Mann-Whitney`=MH, `Brunner-Munzel`=BM, check.names = FALSE)
  }) -> res
  colSums(res)/iter_num
}) -> result

library(tidyr)
library(dplyr)
data <- result %>% data.frame(check.names = FALSE) %>% 
  cbind(sigma=factor(sigma_ratio, levels=sigma_ratio)) %>% 
  gather(`Test Method`, `Alpha Error Rate`, 1:4)

library(ggplot2)
ggplot(data, aes(x=sigma, y=`Alpha Error Rate`, group=`Test Method`, color=`Test Method`)) + 
  geom_line() + geom_point() + ggtitle("Normal Dist.")

有意水準 0.05 で検定を行っているため、alpha error rate はどれも 0.05 になるはずですが、異なる標準偏差に対する検定において、Student と Mann-Whitney は 0.05 から大きく外れており、検定精度が非常に悪いという結果になりました。
対して、Welch と Brunner-Munzel は異なる標準偏差に対しても alpha error rate は 0.05 を保っており、検定精度は非常に良いです。
ここらへんはまあ、理論通りですね。

2. 連続一様分布

それでは、正規性の仮定が崩れた場合はどうなるでしょうか？
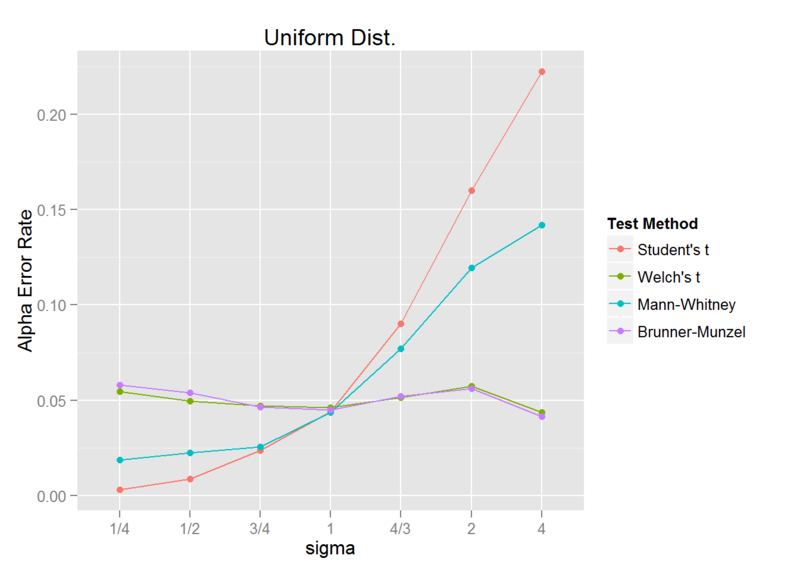
続いては、連続一様分布に対して、先ほどの正規分布と同じ内容のシミュレーションを行ってみます。
すなわち、標準偏差 1 の連続一様分布に対して、標準偏差を 1/4, 1/2, 3/4, 1, 4/3, 2, 4 と変化させた連続一様分布との検定をそれぞれ繰り返し、第一種の過誤を調査します。

sigma_ratio <- c("1/4", "1/2", "3/4", "1", "4/3", "2", "4")
sigma1 <- c(1/4, 1/2, 3/4, 1, 4/3, 2, 4)
a1 <- 5 - sqrt(3) * sigma1
b1 <- 5 + sqrt(3) * sigma1
a2 <- 5 - sqrt(3)
b2 <- 5 + sqrt(3)
iter_num <- 2000

library(pforeach)
library(lawstat)
pforeach(a=a1, b=b1, .c=rbind)({
  npforeach(i=seq_len(iter_num), .c=rbind)({
    x1 <- runif(15, min = a, max = b)
    x2 <- runif(45, min = a2, max = b2)
    student <- t.test(x1, x2, var.equal = TRUE)$p.value <= 0.05
    welch <- t.test(x1, x2, var.equal = FALSE)$p.value <= 0.05
    MH <- wilcox.test(x1,x2)$p.value <= 0.05
    BM <- brunner.munzel.test(x1, x2)$p.value <= 0.05
    data.frame(`Student's t`=student, `Welch's t`=welch, `Mann-Whitney`=MH, `Brunner-Munzel`=BM, check.names = FALSE)
  }) -> res
  colSums(res)/iter_num
}) -> result

library(tidyr)
library(dplyr)
data <- result %>% data.frame(check.names = FALSE) %>% 
  cbind(sigma=factor(sigma_ratio, levels=sigma_ratio)) %>% 
  gather(`Test Method`, `Alpha Error Rate`, 1:4)

library(ggplot2)
ggplot(data, aes(x=sigma, y=`Alpha Error Rate`, group=`Test Method`, color=`Test Method`)) + 
  geom_line() + geom_point() + ggtitle("Uniform Dist.")

結果は、正規分布の場合と同様になりました。
異なる標準偏差に対しては、Student と Mann-Whitney は検定精度が非常に悪く、Welch と Brunner-Munzel は良い精度を保っています。
実は、Welch の t 検定は、ある程度の分布のゆがみに対しても、高い精度を維持できることが知られています。*1
したがって、正規分布が仮定できない場合でも、Mann-Whitney より Welch を使用したほうが良いとする人たちもいます。

3. 対数正規分布(平均値が同じ場合)

上記 2つは対称分布でしたが、歪んだ分布に対する調査として、対数正規分布を考えます。
対数正規分布は、平均値と中央値が異なります。
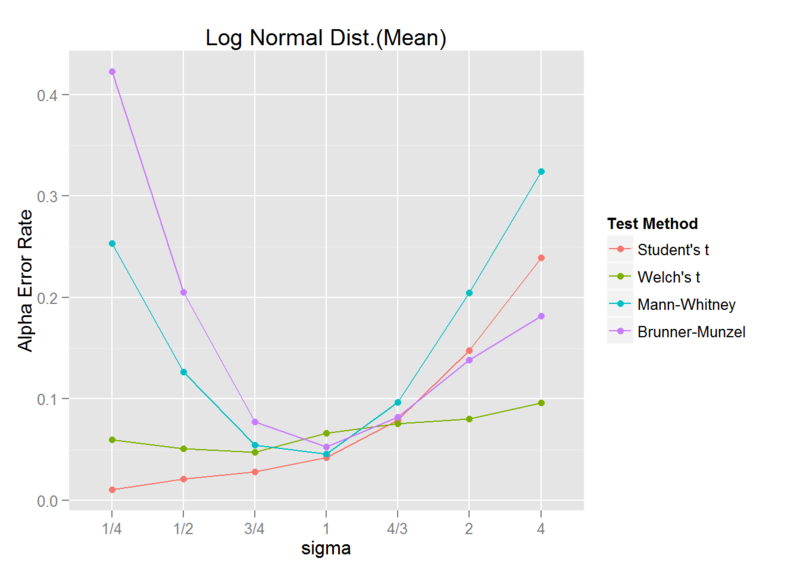
まずは、平均値が同じ対数正規分布について、標準偏差が 1/4, 1/2, 3/4, 1, 4/3, 2, 4 倍となったときの、第一種の過誤を調査します。

sigma_ratio <- c("1/4", "1/2", "3/4", "1", "4/3", "2", "4")
sigma1 <- c(1, 2, 3, 4, 4, 4, 4)
sigma2 <- c(4, 4, 4, 4, 3, 2, 1)
sigmas1 <- sqrt(log((sigma1^2)/(5^2) + 1))
sigmas2 <- sqrt(log((sigma2^2)/(5^2) + 1))
mus1 <- log(5) - (sigmas1^2)/2
mus2 <- log(5) - (sigmas2^2)/2
iter_num <- 2000

library(pforeach)
library(lawstat)
pforeach(mu1=mus1, sigma1=sigmas1, mu2=mus2, sigma2=sigmas2, .c=rbind)({
  npforeach(i=seq_len(iter_num), .c=rbind)({
    x1 <- rlnorm(15, meanlog = mu1, sdlog = sigma1)
    x2 <- rlnorm(45, meanlog = mu2, sdlog = sigma2)
    student <- t.test(x1, x2, var.equal = TRUE)$p.value <= 0.05
    welch <- t.test(x1, x2, var.equal = FALSE)$p.value <= 0.05
    MH <- wilcox.test(x1,x2)$p.value <= 0.05
    BM <- brunner.munzel.test(x1, x2)$p.value <= 0.05
    data.frame(`Student's t`=student, `Welch's t`=welch, `Mann-Whitney`=MH, `Brunner-Munzel`=BM, check.names = FALSE)
  }) -> res
  colSums(res)/iter_num
}) -> result

library(tidyr)
library(dplyr)
data <- result %>% data.frame(check.names = FALSE) %>% 
  cbind(sigma=factor(sigma_ratio, levels=sigma_ratio)) %>% 
  gather(`Test Method`, `Alpha Error Rate`, 1:4)

library(ggplot2)
ggplot(data, aes(x=sigma, y=`Alpha Error Rate`, group=`Test Method`, color=`Test Method`)) + 
  geom_line() + geom_point() + ggtitle("Log Normal Dist.(Mean)")

Student と Mann-Whitney の検定精度が悪いのはこれまでと同様ですが、Brunner-Munzel についても検定精度が悪くなっています。
また、Welch は善戦しているものの、やはり検定精度はあまり良くありません。

4. 対数正規分布(中央値が同じ場合)

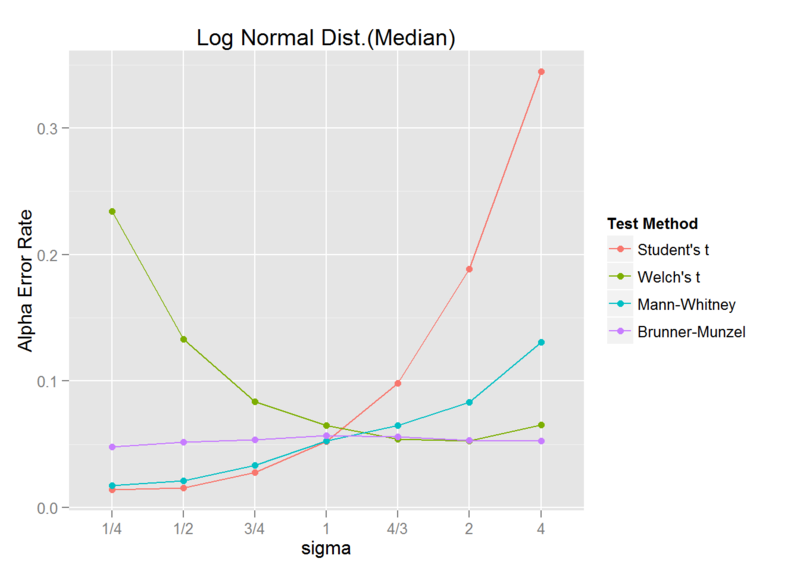
次に、中央値が同じ対数正規分布についても同様に、標準偏差が 1/4, 1/2, 3/4, 1, 4/3, 2, 4 倍となったときの、第一種の過誤を調査します。

sigma_ratio <- c("1/4", "1/2", "3/4", "1", "4/3", "2", "4")
sigma1 <- c(1, 2, 3, 4, 4, 4, 4)
sigma2 <- c(4, 4, 4, 4, 3, 2, 1)
sigmas1 <- sqrt(log((1 + sqrt((4 * sigma1^2)/25 + 1))/2))
sigmas2 <- sqrt(log((1 + sqrt((4 * sigma2^2)/25 + 1))/2))
mu1 <- log(5)
mu2 <- log(5)
iter_num <- 2000

library(pforeach)
library(lawstat)
pforeach(sigma1=sigmas1, sigma2=sigmas2, .c=rbind)({
  npforeach(i=seq_len(iter_num), .c=rbind)({
    x1 <- rlnorm(15, meanlog = mu1, sdlog = sigma1)
    x2 <- rlnorm(45, meanlog = mu2, sdlog = sigma2)
    student <- t.test(x1, x2, var.equal = TRUE)$p.value <= 0.05
    welch <- t.test(x1, x2, var.equal = FALSE)$p.value <= 0.05
    MH <- wilcox.test(x1,x2)$p.value <= 0.05
    BM <- brunner.munzel.test(x1, x2)$p.value <= 0.05
    data.frame(`Student's t`=student, `Welch's t`=welch, `Mann-Whitney`=MH, `Brunner-Munzel`=BM, check.names = FALSE)
  }) -> res
  colSums(res)/iter_num
}) -> result

library(tidyr)
library(dplyr)
data <- result %>% data.frame(check.names = FALSE) %>% 
  cbind(sigma=factor(sigma_ratio, levels=sigma_ratio)) %>% 
  gather(`Test Method`, `Alpha Error Rate`, 1:4)

library(ggplot2)
ggplot(data, aes(x=sigma, y=`Alpha Error Rate`, group=`Test Method`, color=`Test Method`)) + 
  geom_line() + geom_point() + ggtitle("Log Normal Dist.(Median)")

今度は、Welch の検定精度が悪く、Brunner-Munzel は良い精度を保っています。
これは、Brunner-Munzel が「両群から一つずつ値を取り出したとき、どちらが大きい確率も等しいという帰無仮説を検定する」ため、平均値でなく中央値の検定となっているためと考えられます。*2

まとめ

不等分散の状況下において、

• Student の t 検定
• Welch の t 検定
• Mann-Whitney の U 検定
• Brunner-Munzel 検定

の 4つの検定手法について、その検定精度を調査しました。

理論通り、Student の t 検定および Mann-Whitney の U 検定は、不等分散の状況下では検定精度が悪くなりました。
Welch の t 検定および Brunner-Munzel 検定は、ある程度ゆがみのない分布に対しては、十分な検定精度を保ちました。
さらに、歪んだ分布に対しても、中央値の検定としてならば、Brunner-Munzel 検定は十分な検定精度を保ちました。
Welch の t 検定は、歪んだ分布に対しては、検定精度はあまりよくありませんでした。

Brunner-Munzel 検定は、歪んだ分布に対して、平均値の検定としては検定精度は Welch よりも悪くなりました。
しかし、歪んだ分布に対して平均値を検定するという状況はあまり無いのではないでしょうか？
したがって、ほとんどの場合において、Brunner-Munzel 検定は最強ということです。
したがって、平均値の検定には Welch、中央値の検定には Brunner-Munzel を使い分けるというのがいいのではないでしょうか。
Brunner-Munzel 検定を覚えておいて損はないです。

このように最強の検定なのですが、Brunner-Munzel 検定は知名度が低いようです。

@hoxo_m 確かこれを作った人が関係しているジャーナルの知名度を上げるために、あえて無名のそのジャーナルに投稿したため、知名度が低いという話だった気がｗ

— motivic (@motivic_) 2015, 1月 23

というわけで、マイナーだけど最強の統計的検定、Brunner-Munzel 検定をもっと使っていきましょう！

以上です。

追記

フリーの統計分析プログラムHADで有名な清水先生に貴重なご意見をいただきました。

Welchの検定は平均値の差の検定なのだから，等中央値のデータで検定精度を検討するのは無意味だと思うのだが・・・　この結果なら平均値ならWelch，中央値ならBrunner-Munzelで，という結論になるはず。最後の結論はちょっと極端だと思う。＞RT

— Hiroshi Shimizu (@simizu706) 2015, 2月 17

うーむ、そうですね。ちょっと盛りすぎました。
平均値の場合は Welch、中央値の場合は Brunner-Munzel と使い分けるのが良さそうです。

さらに言うと、小標本の場合にうまくいかないという問題もあり、並べ替えBrunner-Munzel検定*3のような方法も提案されています。

追記2

フリーの統計分析プログラムHADで Brunner-Munzel 検定ができるようになりました！はやい！

HAD13.100をアップしました。Brunner-Munzel検定ができるようになりました。 http://t.co/bX48q5ZqJh

— Hiroshi Shimizu (@simizu706) 2015, 2月 18

参考

Brunner-Munzel検定
マン・ホイットニーのU検定と不等分散時における代表値の検定法
http://www.researchgate.net/publication/226351592_The_two-sample_t_test_pre-testing_its_assumptions_does_not_pay_off
RPubs - 対数正規分布から、平均値(中央値)と標準偏差を指定して乱数を生成させる

*1:http://www.researchgate.net/publication/226351592_The_two-sample_t_test_pre-testing_its_assumptions_does_not_pay_off

*2:中央値の検定というのは間違いだそうです。 https://twitter.com/simizu706/status/567970403936649216

*3:http://projecteuclid.org/euclid.ejs/1343310300